一起来写个简单的解释器（7）

英文出处：Ruslan’s Blog

• 《一起来写个简单的解释器（1）》
• 《一起来写个简单的解释器（2）》
• 《一起来写个简单的解释器（3）》
• 《一起来写个简单的解释器（4）》
• 《一起来写个简单的解释器（5）》
• 《一起来写个简单的解释器（6）》

正如我上次向你承诺的那样，今天我将会谈谈我们将在整个系列的其余部分中使用的一个核心数据结构，所以系上安全，咱们出发喽！

直到现在，我们已经将我们的解释器（interpreter ）和解析器（parser）代码混合在一起，只要解析器识别出像加法，减法，乘法或除法这样的特定语言结构，解释器就会求的表达式的值。 这种解释器被称为语法制导解释器（*syntax-directed interpreters*）。 他们通常对输入进行一次遍历，适用于基本的语言应用程序。 为了分析更复杂的Pascal的编程语言结构，我们需要建立一个中间表示（intermediate representation，IR）。 解析器将负责构建一个IR，而解释器将用来解释表示为IR的输入。

事实证明，树是一个非常合适IR的数据结构。

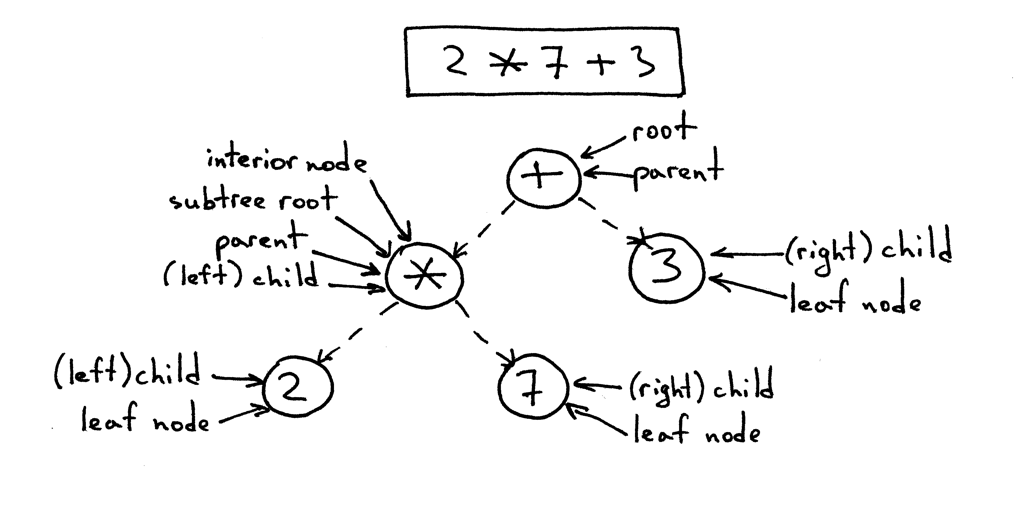
让我们快速谈论树这个术语。

• 树是一个数据结构，由一个或多个组织成层次结构的节点组成。
• 树有一个根节点，这是最顶层的节点。
• 除跟节点之外的所有节点都有唯一的父节点。
• 下图中标有*的节点是一个节点。 标有2和7的节点是他的孩子节点; 孩子节点从左到右排列。
• 没有孩子的节点称为叶节点。
• 具有一个或多个子节点并且不是根的节点称为内部节点。
• 孩子们也可以是完整的子树。 在下面的图片中+节点的左孩子（标有*）是一个有自己孩子节点的完整子树。
• 在计算机科学中，我们从顶部的根节点开始画,树向下生长。

下面是表达式2*7+3的树结构说明

我们将在整个系列中使用的IR被称为抽象语法树（AST），但在深入研究AST之前，我们先来简单地分析树。虽然我们不会为解释器和编译器使用分析树，但它可以帮助您通过可视化解析器的执行轨迹来了解解析器如何解释输入。我们也将它与AST进行比较，看看为什么AST比分析树更适合中间表示。

那么，什么是分析树？分析树（有时称为具体语法树）是一种树，它根据我们的语法定义来表示语言的语法结构。它基本上显示了解析器如何识别语言结构，或者换句话说，它显示了如何在编程语言中某些字符串得到语法的起始符号。

解析器的调用堆栈隐式地表示了一个分析树，当解析器尝试识别特定的语言构造时，它会自动在解析器的内存中构建这个分析树。

让我们看一下表达式2 * 7 + 3的分析树：

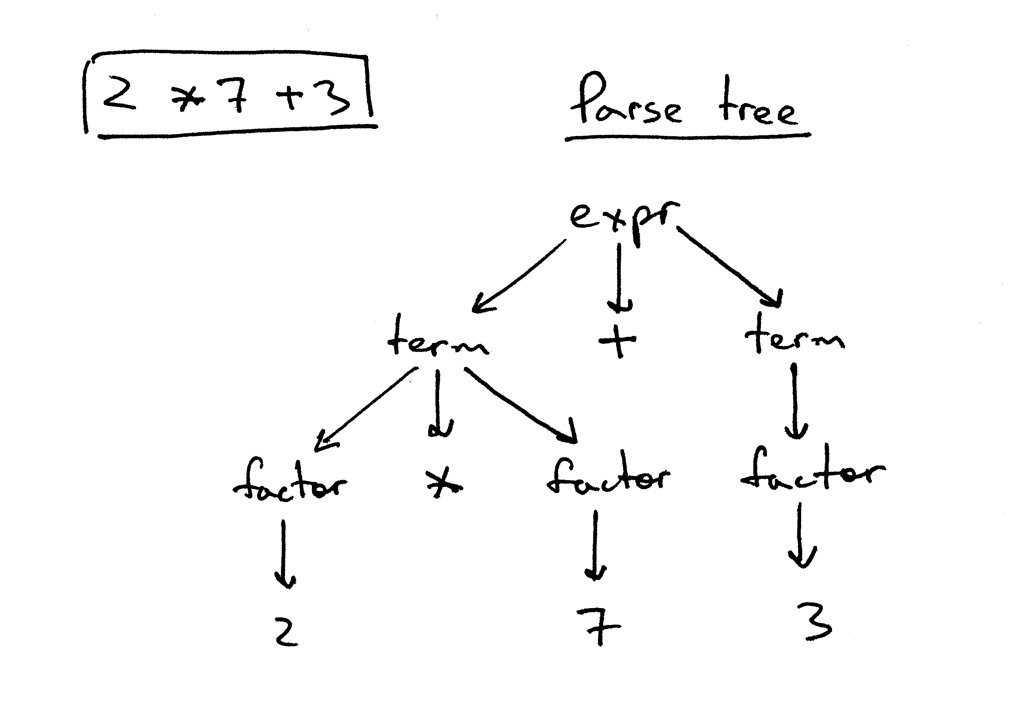
在上图中可以看到：

• 分析树记录了解析器用于识别输入的一系列规则。
• 分析树的根部标有语法开始符号。
• 每个内部节点表示一个非终结符，它代表一个语法规则应用，就像我们的例子中的expr，term或factor。
• 每个叶节点表示一个token。

正如我已经提到的，我们不打算手动构建分析树并将其用于我们的解释器，但解析树可以帮助您通过可视化解析器调用序列来了解解析器如何解释输入。

您可以通过尝试一个名为genptdot.py的实用小程序来查看不同算术表达式的分析树的样子，我很快就写了这个程序来帮助您可视化它们。要使用该程序，您首先需要安装Graphviz包，运行以下命令后，可以打开生成的图像文件parsetree.png，并查看您作为命令行参数传递的表达式的分析树：

$ python genptdot.py "14 + 2 * 3 - 6 / 2" > \
  parsetree.dot && dot -Tpng -o parsetree.png parsetree.dot

这是表达式14 + 2 * 3 - 6 / 2产生的图像文件parsetree.png

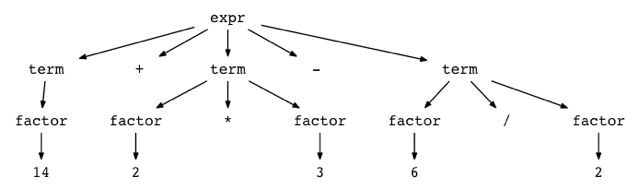
传递不同的算术表达式来试验下程序，看看特定表达式的分析树长什么样。

现在，我们来说说抽象语法树（AST），这是我们将在整个系列的其余部分大量使用的中间表示（IR）。 它是我们解释器和未来编译器项目的核心数据结构之一。

让我们通过查看表达式2 * 7 + 3的AST和分析树开始我们的讨论：

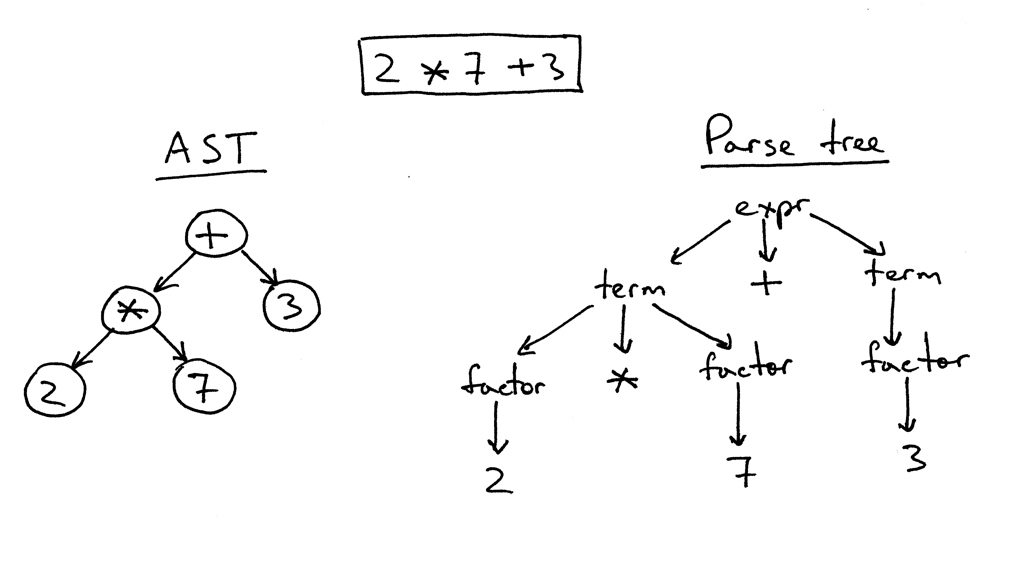
正如你从上面的图片中可以看到的，AST更小的同时抓住了输入的本质。

这里是AST和分析树之间的主要区别：

• AST使用运算符/运算作为根节点和内部节点，并使用操作数作为孩子子节点。
• 与分析树不同，AST不使用内部节点来表示语法规则。
• AST不表示真实语法中的每个细节（这就是为什么他们被称为抽象），例如，没有规则节点和括号。
• 与分析树相比，表示相同语言构造时，AST比较密集。

那么，究竟什么是抽象语法树？抽象语法树（AST）是一种表示语言结构的抽象语法结构的树，每个内部节点和根节点代表一个运算符，他的孩子节点表示该运算符的运算对象。

我已经提到AST比分析树更紧凑。让我们来看看表达式7 +((2 + 3))的AST和分析树。你可以看到下面的AST比分析树小得多，但是仍然抓住了输入的实质：

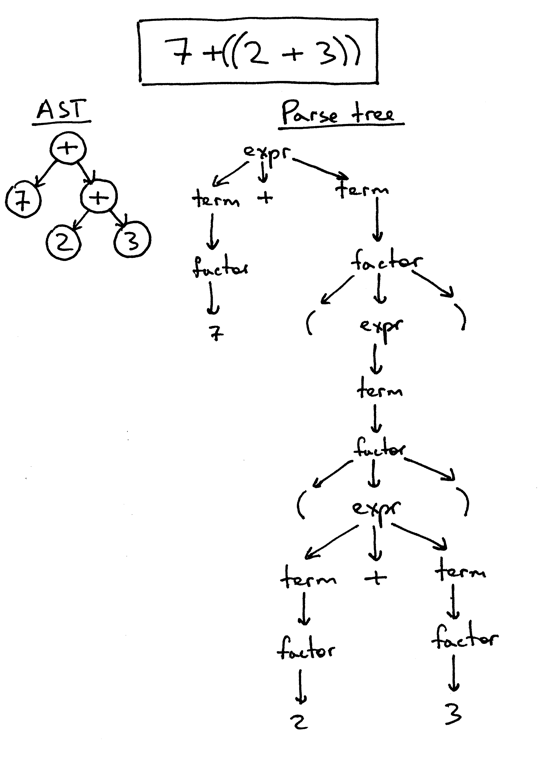
到目前为止都挺棒的，但是如何在AST中对运算符优先级进行编码呢？ 为了在AST中对运算符的优先级进行编码，也就是说，为了表示“X发生在Y之前”，只需在树中将X放在Y下方。在前面的图片中你可以看到这一点。

让我们看看更多的例子。

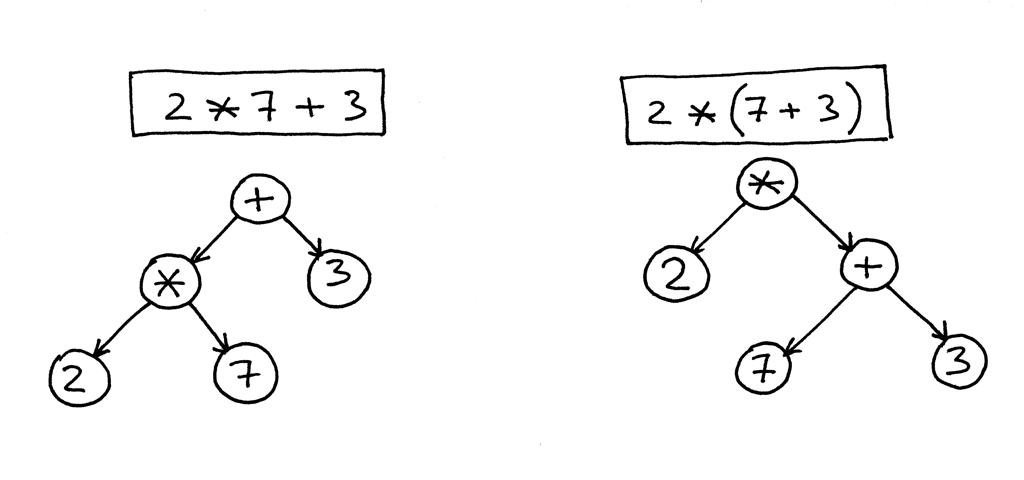
在下面的左侧图片中，可以看到表达式2 * 7 + 3的AST。让我们把7 + 3放在括号内来改变优先级。 您可以在右侧看到修改后表达式2 * (7 + 3)的AST：

这是表达式1 + 2 + 3 + 4 + 5的AST：

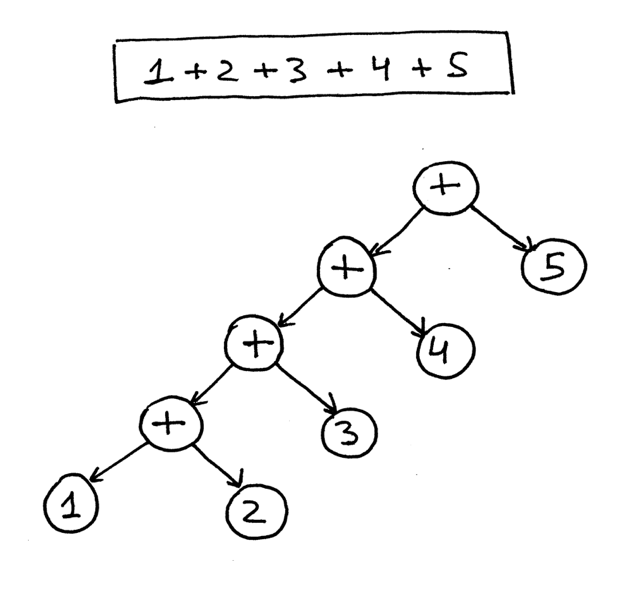
从上面的图片可以看出，优先级较高的操作符在树中较低的位置。

好了，让我们写些代码来实现不同的AST节点类型，并修改我们的解析器以生成由这些节点组成的AST树。

首先，我们将创建一个名为AST的基本节点类，其他类将继承图：

class AST(object):
    pass

实际上并不多。 回想一下，AST代表运算符-运算对象模型。 目前为止，我们有四个运算符和整数运算对象。 运算符是加，减，乘和除。 我们可以分开创建单独的类来表示每个运算符，像AddNode，SubNode，MulNode和DivNode，但相反，我们将只有一个*BinOp*类来表示所有的四个二元运算符（二元运算符是对两个运算对象进行运算的运算符）：

class BinOp(AST):
    def __init__(self, left, op, right):
        self.left = left
        self.token = self.op = op
        self.right = right

构造函数的参数是*left*，*op*和*right*，*left*和*right*相应地指向左操作数的节点和右操作数的节点。 *Op*为运算符本身保留一个令牌：Token(PLUS, ‘+’)用于加号运算符，Token(MINUS, ‘-’) 用于减号运算符，以此类推。

为了表示AST中的整数，我们将定义一个类*Num*，它将保存一个INTEGER标记和标记的值：

class Num(AST):
    def __init__(self, token):
        self.token = token
        self.value = token.value

像你所注意到的，所有节点都存储用于创建节点的令牌。 这主要是为了方便，将来会派上用场。

回想一下表达式2 * 7 + 3的AST。我们将手动创建该表达式的代码：

>>> from spi import Token, MUL, PLUS, INTEGER, Num, BinOp
>>>
>>> mul_token = Token(MUL, '*')
>>> plus_token = Token(PLUS, '+')
>>> mul_node = BinOp(
...     left=Num(Token(INTEGER, 2)),
...     op=mul_token,
...     right=Num(Token(INTEGER, 7))
... )
>>> add_node = BinOp(
...     left=mul_node,
...     op=plus_token,
...     right=Num(Token(INTEGER, 3))
... )

这是我们新的节点类定义的AST的样子，下面的图片也遵循上面的手动构建过程：

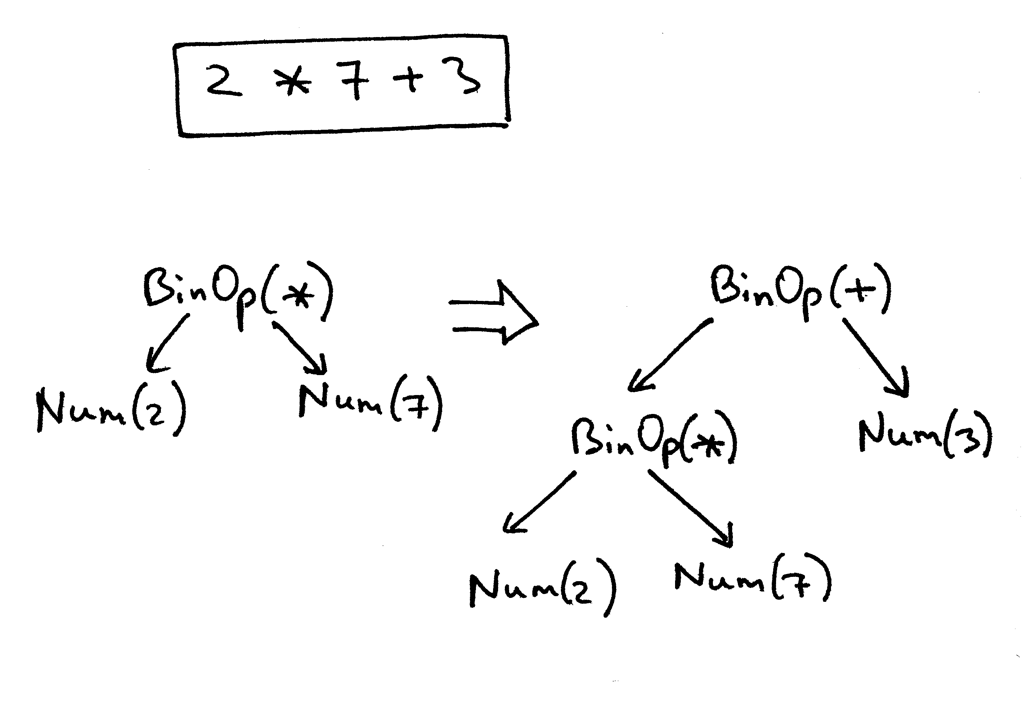
这是我们修改的解析器代码，它通过识别输入（算术表达式）来构建和返回AST：

class AST(object):
    pass


class BinOp(AST):
    def __init__(self, left, op, right):
        self.left = left
        self.token = self.op = op
        self.right = right


class Num(AST):
    def __init__(self, token):
        self.token = token
        self.value = token.value


class Parser(object):
    def __init__(self, lexer):
        self.lexer = lexer
        # set current token to the first token taken from the input
        self.current_token = self.lexer.get_next_token()

    def error(self):
        raise Exception('Invalid syntax')

    def eat(self, token_type):
        # compare the current token type with the passed token
        # type and if they match then "eat" the current token
        # and assign the next token to the self.current_token,
        # otherwise raise an exception.
        if self.current_token.type == token_type:
            self.current_token = self.lexer.get_next_token()
        else:
            self.error()

    def factor(self):
        """factor : INTEGER | LPAREN expr RPAREN"""
        token = self.current_token
        if token.type == INTEGER:
            self.eat(INTEGER)
            return Num(token)
        elif token.type == LPAREN:
            self.eat(LPAREN)
            node = self.expr()
            self.eat(RPAREN)
            return node

    def term(self):
        """term : factor ((MUL | DIV) factor)*"""
        node = self.factor()

        while self.current_token.type in (MUL, DIV):
            token = self.current_token
            if token.type == MUL:
                self.eat(MUL)
            elif token.type == DIV:
                self.eat(DIV)

            node = BinOp(left=node, op=token, right=self.factor())

        return node

    def expr(self):
        """
        expr   : term ((PLUS | MINUS) term)*
        term   : factor ((MUL | DIV) factor)*
        factor : INTEGER | LPAREN expr RPAREN
        """
        node = self.term()

        while self.current_token.type in (PLUS, MINUS):
            token = self.current_token
            if token.type == PLUS:
                self.eat(PLUS)
            elif token.type == MINUS:
                self.eat(MINUS)

            node = BinOp(left=node, op=token, right=self.term())

        return node

    def parse(self):
        return self.expr()

让我们来看看一些算法表达式AST的构造过程。

如果您看了上面的解析器代码，您可以看到它构建AST节点的方式是每个BinOp节点都采用*node*变量的当前值作为其左子节点，并将调用*term*或*factor*的结果作为其 右节点，所以它总是将节点向左下推，下面表达式1 + 2 + 3 + 4 + 5的树就是一个很好的例子。 下面是解析器如何为表达式1 + 2 + 3 + 4 + 5逐步构建AST的可视化展示：

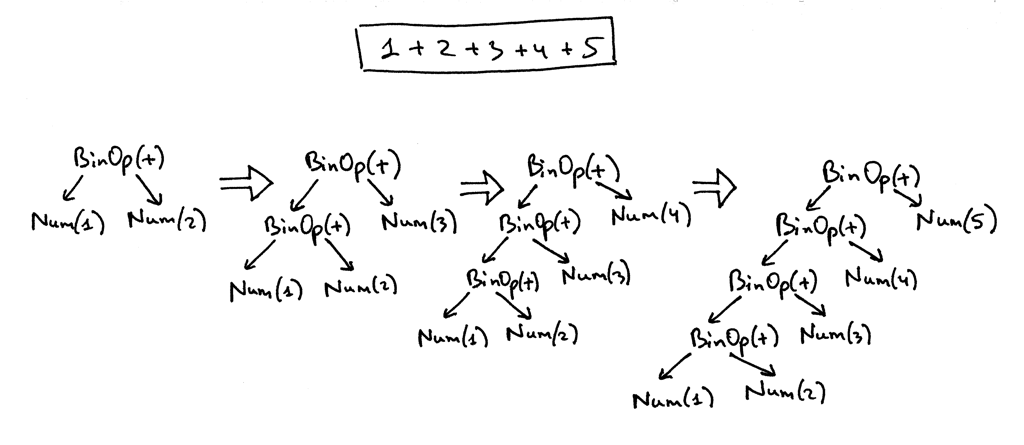
为了帮助您将不同算术表达式的AST可视化，我编写了一个小程序，它将算术表达式作为第一个参数，并生成一个DOT文件，然后由*dot*程序处理以便绘制一个AST（*dot*是 Graphviz软件的一部分，你需要安装并运行dot命令）。 这里是一个命令，并为表达式7 + 3 * (10 / (12 / (3 + 1) - 1))生成AST图片：

$ python genastdot.py "7 + 3 * (10 / (12 / (3 + 1) - 1))" > \
  ast.dot && dot -Tpng -o ast.png ast.dot

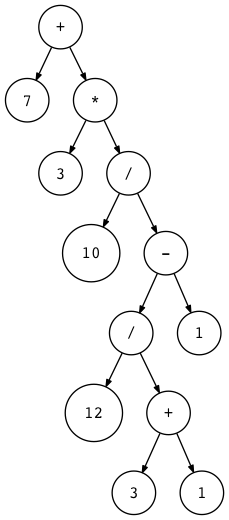
写一些算术表达式，手动绘制它们的AST，然后用genastdot.py工具生成相同表达式的AST图像来验证它们是值得的。 这将帮助您更好地理解解析器如何为不同的算术表达式构造AST。

Okay，下面是表达式2 * 7 + 3的AST：

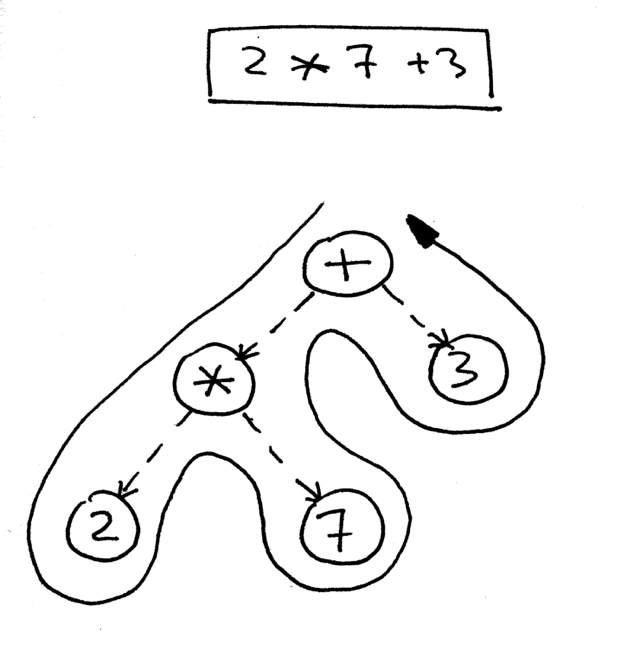
如何操作树来正确地计算树所代表的表达式的值？你可以通过使用后序遍历（深度优先遍历的特殊情况），从根节点开始，递归地从左到右访问每个节点的子节点。后序遍历尽可能快地访问离根最远的节点。

这是后序遍历的伪代码，其中*<< postorder actions >>*是占位符，可能是*BinOp*节点的加减乘除操作，或是返回*Num*节点整数值的操作：

我们要在解释器用后序遍历的原因是：首先，我们需要先计算树中较低的内部节点的值，因为它们是具有较高优先级的运算符；其次，我们需要在使用运算符的运算对象之前计算它的运算对象的值。 在下面的图片中，可以看到，对于后序遍历，我们首先计算表达式2 * 7，然后才计算14 + 3，得到了正确的结果17：

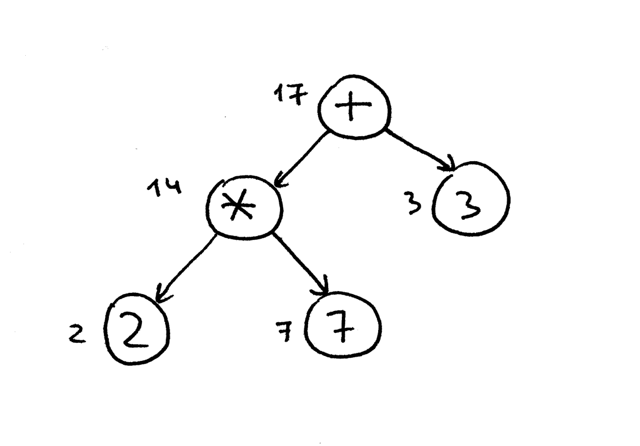
为了完整起见，深度优先遍历有三种类型：前序遍历，中序遍历和后序遍历。遍历方法的名称来自在访问代码中放置操作的地方：

有时你可能需要在所有这些位置上执行某些操作（前序，中序和后序），您将在本文的源代码库中看到一些示例。

Okay，让我们编写一些代码来访问和解释解析器构建的抽象语法树！

这是访问者模式的实现代码：

class NodeVisitor(object):
    def visit(self, node):
        method_name = 'visit_' + type(node).__name__
        visitor = getattr(self, method_name, self.generic_visit)
        return visitor(node)

    def generic_visit(self, node):
        raise Exception('No visit_{} method'.format(type(node).__name__))

这是解释器类的源代码，它继承自*NodeVisitor*类，实现了形如*visit_NodeType*的不同方法，其中*NodeType*是节点的类名如*BinOp*，*Num*等：

class Interpreter(NodeVisitor):
    def __init__(self, parser):
        self.parser = parser

    def visit_BinOp(self, node):
        if node.op.type == PLUS:
            return self.visit(node.left) + self.visit(node.right)
        elif node.op.type == MINUS:
            return self.visit(node.left) - self.visit(node.right)
        elif node.op.type == MUL:
            return self.visit(node.left) * self.visit(node.right)
        elif node.op.type == DIV:
            return self.visit(node.left) / self.visit(node.right)

    def visit_Num(self, node):
        return node.value

有两个有趣的关于代码事值得一提：首先，操作AST节点的访问者代码与AST节点本身是解耦的。 可以看到，没有任何AST节点类（*BinOp*和*Num*）提供任何代码来操作存储在这些节点中的数据。 该逻辑封装在实现*NodeVisitor*类的*Interprete*r类中。

其次，*NodeVisitor*的*visit*方法中没有像下面展示的那样有大量的if语句：

def visit(node):
    node_type = type(node).__name__
    if node_type == 'BinOp':
        return self.visit_BinOp(node)
    elif node_type == 'Num':
        return self.visit_Num(node)
    elif ...
    # ...

或者这样

def visit(node):
    if isinstance(node, BinOp):
        return self.visit_BinOp(node)
    elif isinstance(node, Num):
        return self.visit_Num(node)
    elif ...

*NodeVisitor*的*visit*方法非常通用，它根据传给它的节点类型来调用适当的方法。正如我之前提到的，为了使用它，我们的解释器继承自*NodeVisitor*类并实现必要的方法。因此，如果传递给*visit*方法的节点的类型是*BinOp*，则*visit*方法将调用到*visit_BinOp*方法，如果节点的类型是*Num*，则访问方法将调用到*visit_Num*方法。

花一些时间研究这种方法（标准Python模块ast使用了相同的机制来进行节点遍历），将来我们将用许多新的*visit_NodeType*方法来扩展我们的解释器。

*generic_visit*方法是一个fallback，它引发一个异常，表明它遇到了一个没有对应的*visit_NodeType*方法的节点。

现在，让我们为表达式2 * 7 + 3手动构建AST，并将其传递给解释器，以查看visit方法以计算表达式。下面是你在Python shell中需要做的：

>>> from spi import Token, MUL, PLUS, INTEGER, Num, BinOp
>>>
>>> mul_token = Token(MUL, '*')
>>> plus_token = Token(PLUS, '+')
>>> mul_node = BinOp(
...     left=Num(Token(INTEGER, 2)),
...     op=mul_token,
...     right=Num(Token(INTEGER, 7))
... )
>>> add_node = BinOp(
...     left=mul_node,
...     op=plus_token,
...     right=Num(Token(INTEGER, 3))
... )
>>> from spi import Interpreter
>>> inter = Interpreter(None)
>>> inter.visit(add_node)
17

正如你所看到的，我将表达式树的根传递给*visit*方法，并通过调用*Interpreter*类的正确方法（*visit_BinOp*和*visit_Num*）来遍历树，并获得结果。

好的，下面是我们新解释器的完整代码，以方便您使用：

""" SPI - Simple Pascal Interpreter """

###############################################################################
#                                                                             #
#  LEXER                                                                      #
#                                                                             #
###############################################################################

# Token types
#
# EOF (end-of-file) token is used to indicate that
# there is no more input left for lexical analysis
INTEGER, PLUS, MINUS, MUL, DIV, LPAREN, RPAREN, EOF = (
    'INTEGER', 'PLUS', 'MINUS', 'MUL', 'DIV', '(', ')', 'EOF'
)


class Token(object):
    def __init__(self, type, value):
        self.type = type
        self.value = value

    def __str__(self):
        """String representation of the class instance.

        Examples:
            Token(INTEGER, 3)
            Token(PLUS, '+')
            Token(MUL, '*')
        """
        return 'Token({type}, {value})'.format(
            type=self.type,
            value=repr(self.value)
        )

    def __repr__(self):
        return self.__str__()


class Lexer(object):
    def __init__(self, text):
        # client string input, e.g. "4 + 2 * 3 - 6 / 2"
        self.text = text
        # self.pos is an index into self.text
        self.pos = 0
        self.current_char = self.text[self.pos]

    def error(self):
        raise Exception('Invalid character')

    def advance(self):
        """Advance the `pos` pointer and set the `current_char` variable."""
        self.pos += 1
        if self.pos > len(self.text) - 1:
            self.current_char = None  # Indicates end of input
        else:
            self.current_char = self.text[self.pos]

    def skip_whitespace(self):
        while self.current_char is not None and self.current_char.isspace():
            self.advance()

    def integer(self):
        """Return a (multidigit) integer consumed from the input."""
        result = ''
        while self.current_char is not None and self.current_char.isdigit():
            result += self.current_char
            self.advance()
        return int(result)

    def get_next_token(self):
        """Lexical analyzer (also known as scanner or tokenizer)

        This method is responsible for breaking a sentence
        apart into tokens. One token at a time.
        """
        while self.current_char is not None:

            if self.current_char.isspace():
                self.skip_whitespace()
                continue

            if self.current_char.isdigit():
                return Token(INTEGER, self.integer())

            if self.current_char == '+':
                self.advance()
                return Token(PLUS, '+')

            if self.current_char == '-':
                self.advance()
                return Token(MINUS, '-')

            if self.current_char == '*':
                self.advance()
                return Token(MUL, '*')

            if self.current_char == '/':
                self.advance()
                return Token(DIV, '/')

            if self.current_char == '(':
                self.advance()
                return Token(LPAREN, '(')

            if self.current_char == ')':
                self.advance()
                return Token(RPAREN, ')')

            self.error()

        return Token(EOF, None)


###############################################################################
#                                                                             #
#  PARSER                                                                     #
#                                                                             #
###############################################################################

class AST(object):
    pass


class BinOp(AST):
    def __init__(self, left, op, right):
        self.left = left
        self.token = self.op = op
        self.right = right


class Num(AST):
    def __init__(self, token):
        self.token = token
        self.value = token.value


class Parser(object):
    def __init__(self, lexer):
        self.lexer = lexer
        # set current token to the first token taken from the input
        self.current_token = self.lexer.get_next_token()

    def error(self):
        raise Exception('Invalid syntax')

    def eat(self, token_type):
        # compare the current token type with the passed token
        # type and if they match then "eat" the current token
        # and assign the next token to the self.current_token,
        # otherwise raise an exception.
        if self.current_token.type == token_type:
            self.current_token = self.lexer.get_next_token()
        else:
            self.error()

    def factor(self):
        """factor : INTEGER | LPAREN expr RPAREN"""
        token = self.current_token
        if token.type == INTEGER:
            self.eat(INTEGER)
            return Num(token)
        elif token.type == LPAREN:
            self.eat(LPAREN)
            node = self.expr()
            self.eat(RPAREN)
            return node

    def term(self):
        """term : factor ((MUL | DIV) factor)*"""
        node = self.factor()

        while self.current_token.type in (MUL, DIV):
            token = self.current_token
            if token.type == MUL:
                self.eat(MUL)
            elif token.type == DIV:
                self.eat(DIV)

            node = BinOp(left=node, op=token, right=self.factor())

        return node

    def expr(self):
        """
        expr   : term ((PLUS | MINUS) term)*
        term   : factor ((MUL | DIV) factor)*
        factor : INTEGER | LPAREN expr RPAREN
        """
        node = self.term()

        while self.current_token.type in (PLUS, MINUS):
            token = self.current_token
            if token.type == PLUS:
                self.eat(PLUS)
            elif token.type == MINUS:
                self.eat(MINUS)

            node = BinOp(left=node, op=token, right=self.term())

        return node

    def parse(self):
        return self.expr()


###############################################################################
#                                                                             #
#  INTERPRETER                                                                #
#                                                                             #
###############################################################################

class NodeVisitor(object):
    def visit(self, node):
        method_name = 'visit_' + type(node).__name__
        visitor = getattr(self, method_name, self.generic_visit)
        return visitor(node)

    def generic_visit(self, node):
        raise Exception('No visit_{} method'.format(type(node).__name__))


class Interpreter(NodeVisitor):
    def __init__(self, parser):
        self.parser = parser

    def visit_BinOp(self, node):
        if node.op.type == PLUS:
            return self.visit(node.left) + self.visit(node.right)
        elif node.op.type == MINUS:
            return self.visit(node.left) - self.visit(node.right)
        elif node.op.type == MUL:
            return self.visit(node.left) * self.visit(node.right)
        elif node.op.type == DIV:
            return self.visit(node.left) / self.visit(node.right)

    def visit_Num(self, node):
        return node.value

    def interpret(self):
        tree = self.parser.parse()
        return self.visit(tree)


def main():
    while True:
        try:
            try:
                text = raw_input('spi> ')
            except NameError:  # Python3
                text = input('spi> ')
        except EOFError:
            break
        if not text:
            continue

        lexer = Lexer(text)
        parser = Parser(lexer)
        interpreter = Interpreter(parser)
        result = interpreter.interpret()
        print(result)


if __name__ == '__main__':
    main()

将上面的代码保存到*spi.py*文件或直接从GitHub下载。 试试看新的基于树的解释器能否正确地计算算术表达式。

以下是一个示例会话：

$ python spi.py
spi> 7 + 3 * (10 / (12 / (3 + 1) - 1))
22
spi> 7 + 3 * (10 / (12 / (3 + 1) - 1)) / (2 + 3) - 5 - 3 + (8)
10
spi> 7 + (((3 + 2)))
12

今天，您已经学习了解析树、AST、和怎样构建AST以及如何遍历它来解释由这些AST表示的输入。 您还修改了解析器和解释器，并将它们分开。词法分析器，解析器和解释器之间的当前接口如下所示：

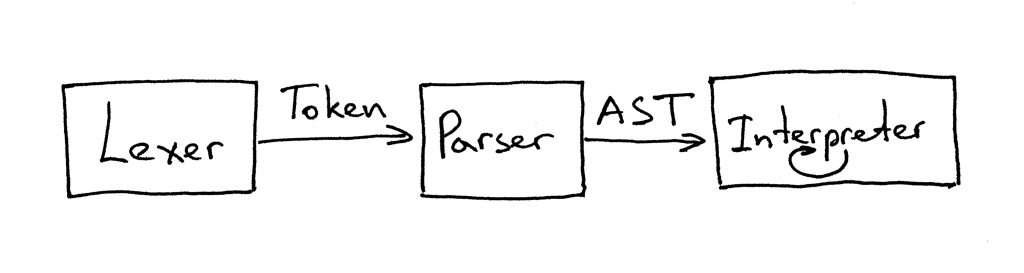
你可以这样理解：“解析器从词法分析器获取标记，然后为解释器返回生成的AST，解释器遍历和解释输入。”

这就是今天的内容，但在结束之前，我想简单地谈一谈递归下降解析器，即给它一个定义，因为我上次答应更详细地讨论它。 递归下降解析器是一个自顶向下的解析器，它使用一组递归过程来处理输入。 自上而下反映了这样的事实：解析器首先构造解析树的顶层节点，然后逐渐构建低层节点。

现在是时候做练习了:)

• 写一个翻译器（提示：node visitor），输入一个算术表达式，并打印其后缀表示法，也被称为逆波兰式（RPN）。 例如，如果翻译器的输入是表达式(5 + 3) * 12 / 3 ，则输出应该是5 3 + 12 * 3 /。 这里是答案，但你应首先尝试自己解决它。
• 写一个翻译器（节点访客），输入一个算术表达式，并以LISP风格的形式打印出来，即2 + 3将变成(+ 2 3)，(2 + 3 * 5)变成(+ 2 (* 3 5))。 您可以在这里找到答案，但同样在查看提供的解决方案之前首先自己尝试解决它。

在下一篇文章中，我们将为我们成长的Pascal解释器的增加赋值和一元运算符。 在此之前，玩得开心，再见。

附： 我还提供了一个可以在GitHub上找到的解释器的Rust实现。 这是我学习Rust的一种方式，所以请记住，代码可能不是很“符合语音习惯”。 欢迎有关如何使代码更好的意见和建议。

以下是我推荐的书籍列表，可以帮助你学习解释器和编译器：

1. Language Implementation Patterns: Create Your Own Domain-Specific and General Programming Languages (Pragmatic Programmers)
2. Writing Compilers and Interpreters: A Software Engineering Approach
3. Modern Compiler Implementation in Java
4. Modern Compiler Design
5. Compilers: Principles, Techniques, and Tools (2nd Edition)

顺便说一下，我正在编写一本叫《Let’s Build A Web Server: First Steps》的书，解释如何从头开始编写基本的Web服务器。你可以在这里，这里和这里查看这本书。